Прямоугольник. онлайн калькулятор

Примеры

Рассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2

пишем treug a=8;C=70;ha=2

Медиана mc на сторону c = 4.4770789813853

Вот и все, все параметры треугольника.

Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой.» А далее нарисовать в уме треугольник, и применить к заданному вопросу.

Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же.

Как рассчитать треугольник если известны координаты его вершин?

Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3

пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3

Источник

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

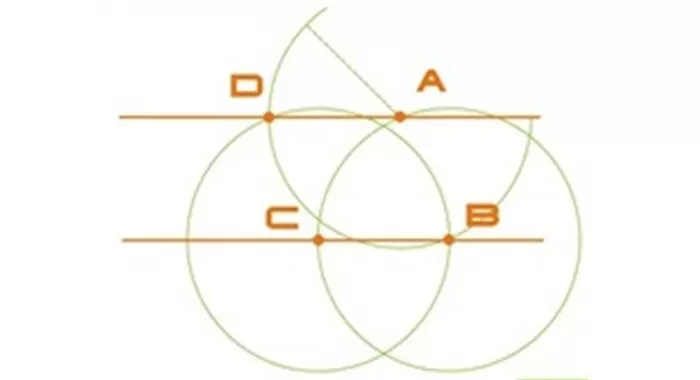
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Задача решена.

Как построить график функции онлайн на этом сайте?

Чтобы построить график функции онлайн, нужно просто ввести свою функцию в специальное поле и кликнуть куда-нибудь вне его. После этого график введенной функции нарисуется автоматически. Допустим, вам требуется построить классический график функции «икс в квадрате». Соответственно, нужно ввести в поле «x^2».

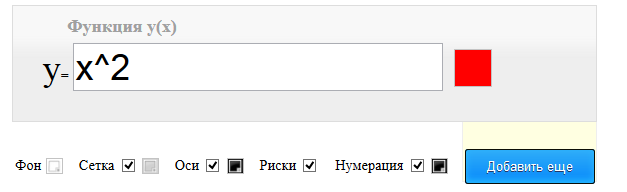
Если вам нужно построить график нескольких функций одновременно, то нажмите на синюю кнопку «Добавить еще». После этого откроется еще одно поле, в которое надо будет вписать вторую функцию. Ее график также будет построен автоматически.

Цвет линий графика вы можете настроить с помощью нажатия на квадратик, расположенный справа от поля ввода функции. Остальные настройки находятся прямо над областью графика. С их помощью вы можете установить цвет фона, наличие и цвет сетки, наличие и цвет осей, наличие рисок, а также наличие и цвет нумерации отрезков графика. Если необходимо, вы можете масштабировать график функции с помощью колесика мыши или специальных иконок в правом нижнем углу области рисунка.

После построения графика и внесения необходимых изменений в настройки, вы можете скачать график с помощью большой зеленой кнопки «Скачать» в самом низу. Вам будет предложено сохранить график функции в виде картинки формата PNG.

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

Из формулы (7) найдем \( \small b \) и подставим в (6):

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Действительно.

Тогда

Имеем \( \small \sqrt{D} <2d ,\) \( \small P > 2d .\) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Znanija — приложение, которое поможет решить уравнение по геометрии

На сайте znanija.com пользователи могут выкладывать фотографии с геометрическими задачками. Это русскоязычный сегмент проекта brainly.com. Он позволяет ученикам обращаться за квалифицированной помощью специалистов со всего мира.

Вы можете найти приложение «Знания» по запросу «Brainly» на платформе App Store или Google Play. Скачайте эту программу на свой телефон, чтобы пообщаться с экспертами и отличниками.

Основные достоинства приложения для решения сложных задач по геометрии:

Преимущества приложения:	Пояснения:
Здесь разбирающиеся в предмете люди могут оказать посильную помощь тем, кто в этом нуждается.	Набирайте за это баллы и получайте увеличение статуса. Чтобы увидеть размер вознаграждения, посмотрите на иконку в правом верхнем углу от вопроса. Наведите на нее курсор, и вы сможете узнать больше о системе баллов.
Если не хотите ожидать ответа, воспользуйтесь поиском по архиву.	В библиотеке «Знания» накопилось уже немало готовых решений задач. Наверняка там найдется и нужная вам информация.
В приложении есть встроенные покупки.	Однако цена годовой подписки на App Store сравнительно невелика.
Сообщество работает круглосуточно.	Пользователи проживают в разных часовых поясах, поэтому могут отвечать на вопросы в любое время.

Для записи геометрических функций и математических знаков работает клавиатура LaTeX.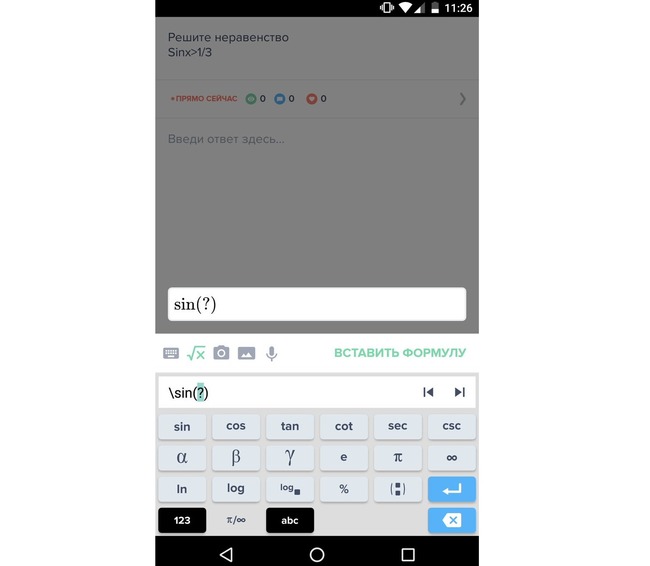

В приложении можно получить помощь по всем базовым предметам, включая геометрию. Доступны такие языки как украинский, казахский, белорусский.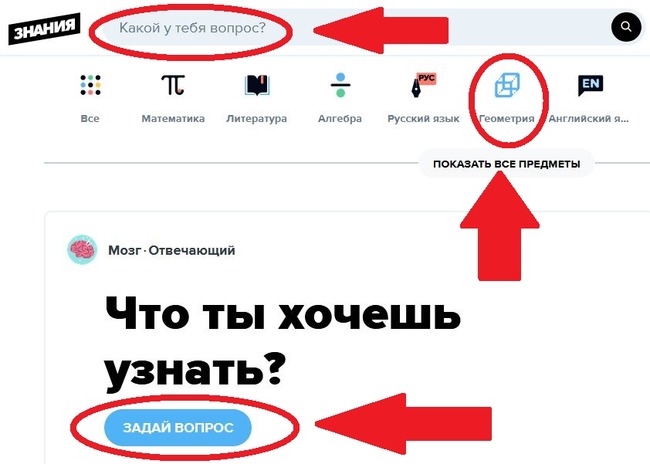

Чтобы вас не ввели в заблуждение, эксперты сообщества просматривают ответы к задачам и оставляют пометку «Проверенный». Если вы ее увидите, то можете полагаться на такой комментарий.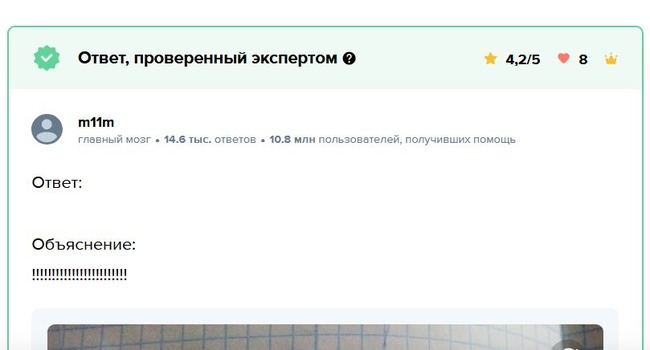

Ответы находятся очень быстро. Решение большинства задач по геометрии находится в течение первых 10 минут с момента загрузки фото в приложение. Однако на всякий случай постарайтесь скидывать снимки заранее. Даже если вы получите ответ сразу, у вас останется больше времени на то, чтобы понять объяснение и подготовиться к уроку.

Onlinecharts.ru

Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:

• Линейные.
• Столбчатые.
• Круговые.
• С областями.
• Радиальные.
• XY-графики.
• Пузырьковые.
• Точечные.
• Полярные бульки.
• Пирамиды.
• Спидометры.
• Столбчато-линейные.

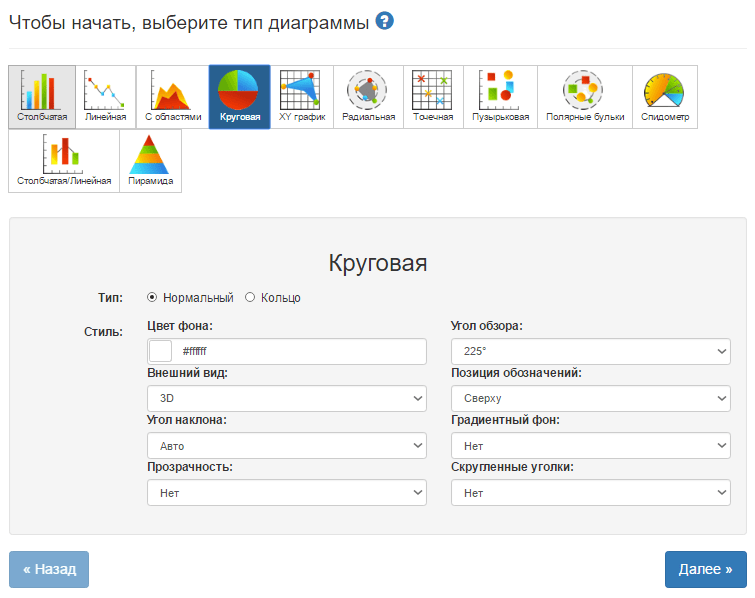
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.

Onshape позволяет работать с файлами .dwg

Англоязычный онлайн-сервис Onshape предлагает профессиональные решения для проектирования и создания чертежей в системе 3D-cad. К сожалению, бесплатный функционал сайта ограничен 21 днём бесплатного пользования, далее же за возможность создавать чертежи онлайн с помощью Onshape необходимо будет платить «живые» деньги.

Для работы с Onshape перейдите на данный ресурс, нажмите на кнопку «I WANT TO TRY ONSHAPE» (если такой кнопки нет, просто перезагрузите главную страницу сайта).

1. Пройдите расширенную регистрацию для работы с AutoCAD онлайн, и вы окажетесь в окне создания и редактирования чертежей.
2. Для создания нового чертежа нажмите на «Create» (создать), укажите имя документа.
3. Выберите уровень доступа к нему («Private» — личный, «Public» — общедоступный) и нажмите на «Ок».

4. Для сохранения вашего чертежа кликните правой клавишей мыши на закладке вашего файла внизу.

5. Выберите «Export», определитесь с форматом исходящего файла, укажите «Download» и нажмите на «Ок».

Упрощённые сервисы для работы с AutoCAD

Также для осуществления черчения онлайн могут помочь такие сервисы как drawisland.com и sketch.io. Функционал указанных сервисов довольно прост, и может пригодиться, скорее, для развлекательных и бытовых целей, нежели для профессионального черчения.

Рабочее окно сервиса Drawisland

LibreCad — это сервис для двумерного проектирования и черчения

Среди богатства возможностей ресурса rollap.com имеется сервис, позволяющий создавать чертежи онлайн. Речь идёт о LibreCad – довольно удобном инструменте, позволяющим проводить 2Д черчение для профессиональных целей. Сервис позволяет работать с SVG, JPG, PNG, PDF файлами, чертить с помощью мышки и клавиатуры, использовать слои, блоки, сплайны, полилинии, имеет функцию текстового редактора и так далее.

1. Для работы с LibreCad перейдите по указанной выше ссылке, и нажмите на кнопку «Launch online» (запуск онлайн).
2. Сервис предложит вам выбрать язык (найдите и выберите «русский») и меру длины (миллиметр).

3. После определения настроек откроется рабочее окно, где вы сможете создать и отредактировать ваш чертёж с помощью соответствующего инструментария.

4. Для сохранения полученного результата необходимо подключение к облачным сервисам (Dropbox, Google Drive, OneDrive или Box), сохранение результата туда, а уже оттуда вы можете скачать ваш чертёж к себе на ПК.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

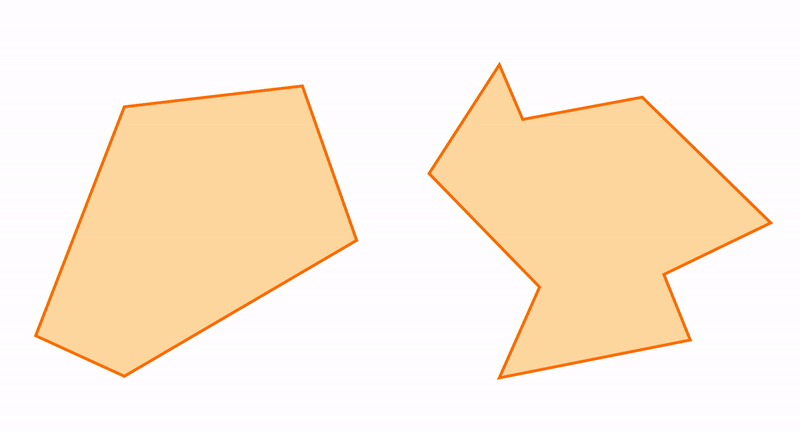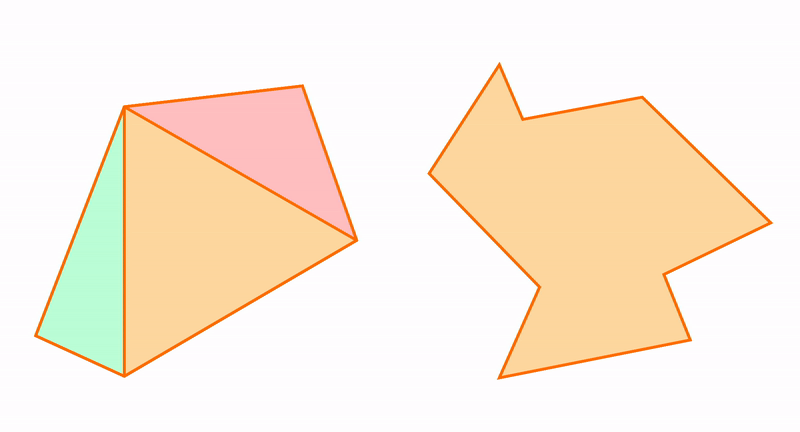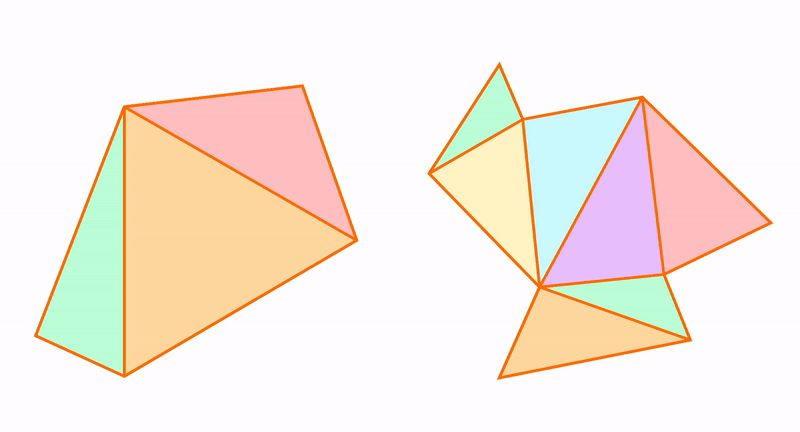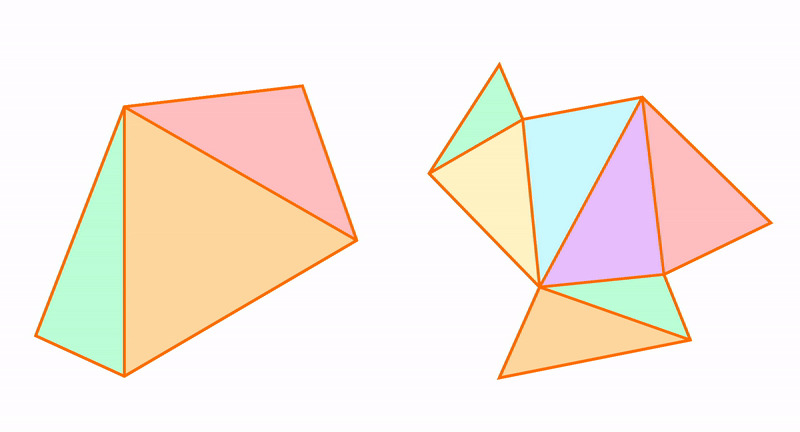
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

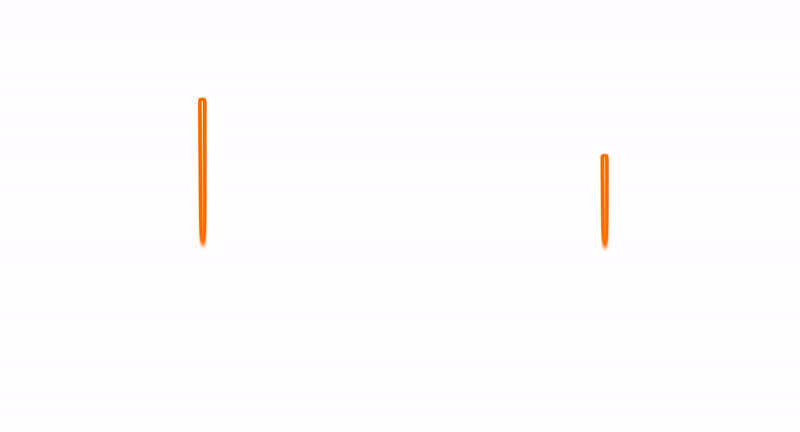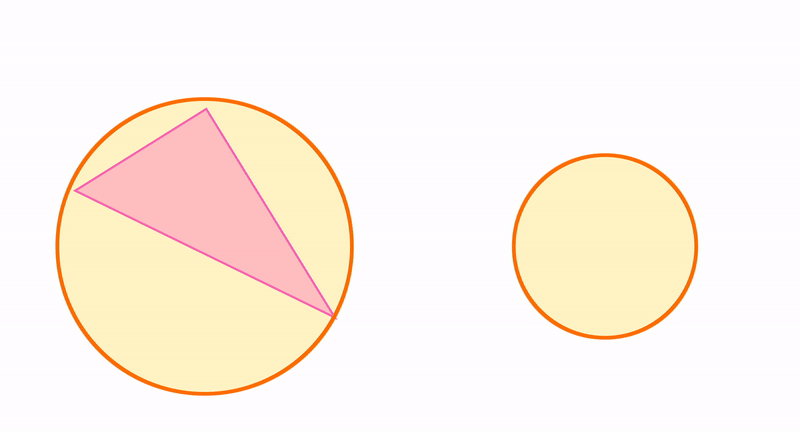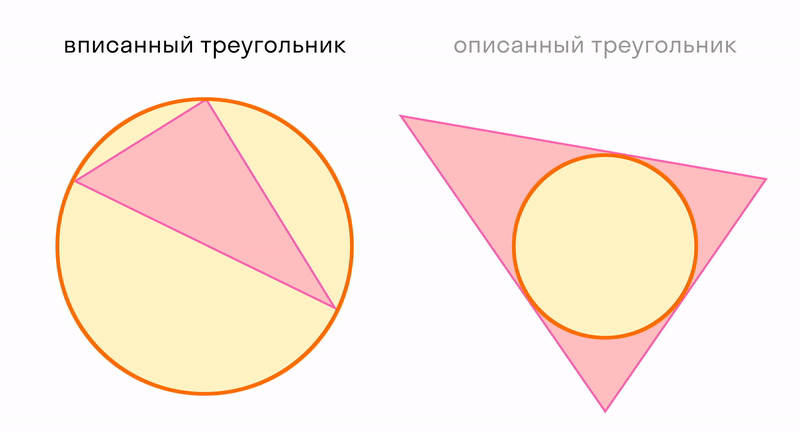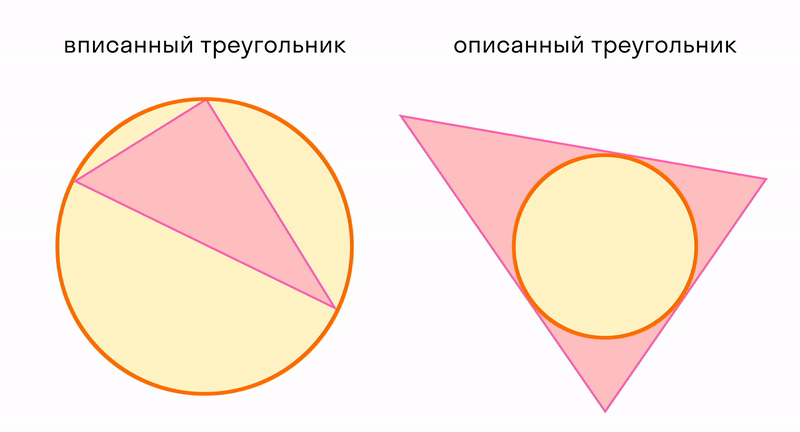
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

• две стороны и угол между ними;
• два угла и сторону;
• три стороны.

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже

Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б

Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Расширение GeoGebra

Создано расширение GeoGebra для браузера Google Chrome

Обратите внимание на количество пользователей расширения: более 2.6 миллиона человек. Немногие расширения из магазина Chrome могут сравниться с такими цифрами

Это свидетельствует о том, что приложение GeoGebra широко используется в мире для образовательных целей.

Для входа в расширение кликните по кнопке «Сервисы» на панели закладок в браузере Google Chrome. После этого будет открыто окно расширения GeoGebra в вашем браузере. На начальном экране вы можете выбрать раздел математики, с которым далее вы будете работать в приложении.

Дополнительные материалы по работе в программе, вы можете найти на сайте производителя приложения, и в интернете.

Тест: Человек из геометрических фигур

1 тип – Руководитель (811, 712, 721, 613, 622, 631)

Это легко приспосабливающиеся личности, готовые руководить и заниматься организацией любой деятельности. Как правило, это прекрасные рассказчики, красноречивые и умеющие поддержать разговор. Любят доминировать, но стараются себя контролировать и не переходить границы с другими.

Довольно активные, не любят сидеть без дела. Придают значение не только результату, но и самому процессу достижения цели. Могут преувеличивать свои успехи и неудачи, и нетерпимы, сталкиваясь с препятствиями на своем пути.

В отношениях они предпочитают занимать главенствующую роль, а в случае конфликта проявляют соперничество.

Любят быть в центре внимания и жаждут признания. В то же время этот тип личности берет ответственность на себя и хочет оправдать ожидания окружающих.

Для них характерна импульсивность, и при принятии решения они действуют в зависимости от настроения. Это может привести к необдуманным решениям и неприятным последствиям.

2 тип – Ответственный исполнитель (514, 523, 532, 541)

Этот тип личности в первую очередь нацелен на совершенствование своих навыков и достижение профессионализма. Такой человек ответственный, может проявлять требовательность, как к себе, так и к другим.

У человека развитое чувство справедливости и стремление к правде

Хотя у него есть хорошие организаторские способности, может сомневаться, если нужно принять важное решение.. К отношениям подходит осмотрительно, проявляет тактичность

Не может отказать, если его о чем-то попросили. Иногда может браться за несколько дел одновременно, полагаясь только на себя, но не всегда верно рассчитывает свои силы. Предпочитает выполнять работу сам, не перепоручая ее другим. Тяжело переживает неудачи.

К отношениям подходит осмотрительно, проявляет тактичность. Не может отказать, если его о чем-то попросили. Иногда может браться за несколько дел одновременно, полагаясь только на себя, но не всегда верно рассчитывает свои силы. Предпочитает выполнять работу сам, не перепоручая ее другим. Тяжело переживает неудачи.

Эти люди отличаются трудолюбием и требовательны к себе, ожидая того же от остальных. В работу включаются постепенно, устойчивы при сильном умственном напряжении, но могут утомляться при высоком темпе работы. Придают большее значение результату, а не процессу деятельности. Всегда стремятся завершить дела.

Внешне такие люди более сдержанны, но могут эмоционально реагировать при изменениях внешних факторов. Им нужно быть острожными, так как из-за перенапряжения есть опасность развития заболеваний нервного характера.

Примеры рисунков человека из геометрических фигур

3 тип – Инициатор (433, 343, 334)

Этот человек обладает философским мышлением, может быть оторван от реальности. Бывает отчужденным, и ему кажется, что он не похож на остальных. В случае трудностей склонны уходить в свой мир фантазий. 

Хотя им не составляет труда установить контакт с другими людьми, они склонны держать определенную дистанцию в общении. Сталкиваясь с конфликтной ситуацией, могут замыкаться в себе, но внешне остаются невозмутимыми.

Отличаются способностями в различных областях, не любят монотонности и избегают рутинной работы. Воодушевляются при смене деятельности и появлении новых возможностей. Стремятся к новизне и могут неожиданно поменять профессию. Этот тип распространен у людей искусства, занимающихся творческой деятельностью, работающих в области рекламы и дизайна.

4 тип – Эмотивный (181, 271, 172, 361, 262, 163)

Этот тип обладает развитой способностью сопереживать другим. Жизненные трудности и даже драматические фильмы могут вызвать у них сильные переживания.

Участливы и неравнодушны к проблемам окружающих. Часто чужие проблемы ставят на первое место, отодвигая на задний план свои потребности. Могут быть импульсивны и действовать под влиянием эмоций. Хотя у них есть способности в разных видах деятельности, лучше всего могут реализоваться, если выбрать какое-то одно направление.

В отношениях проявляют чувствительность, тяжело переживают неурядицы и разрывы отношений.

Отношения с окружающими в целом строят легко и не выходят за рамки принятых норм поведения

Им важно, как их самих и их деятельность оценивают окружающие.

Интерфейс GeoGebra

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.

Давайте рассмотрим основные элементы интерфейса программы GeoGebra:

1. Полоса меню. Из меню вы можете изменить настройки программы.
2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
4. Кнопки «Отменить» и «Повторить».
5. Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra.

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

∠ А = A₁, ∠ В = B₁, ∠ С = C₁,

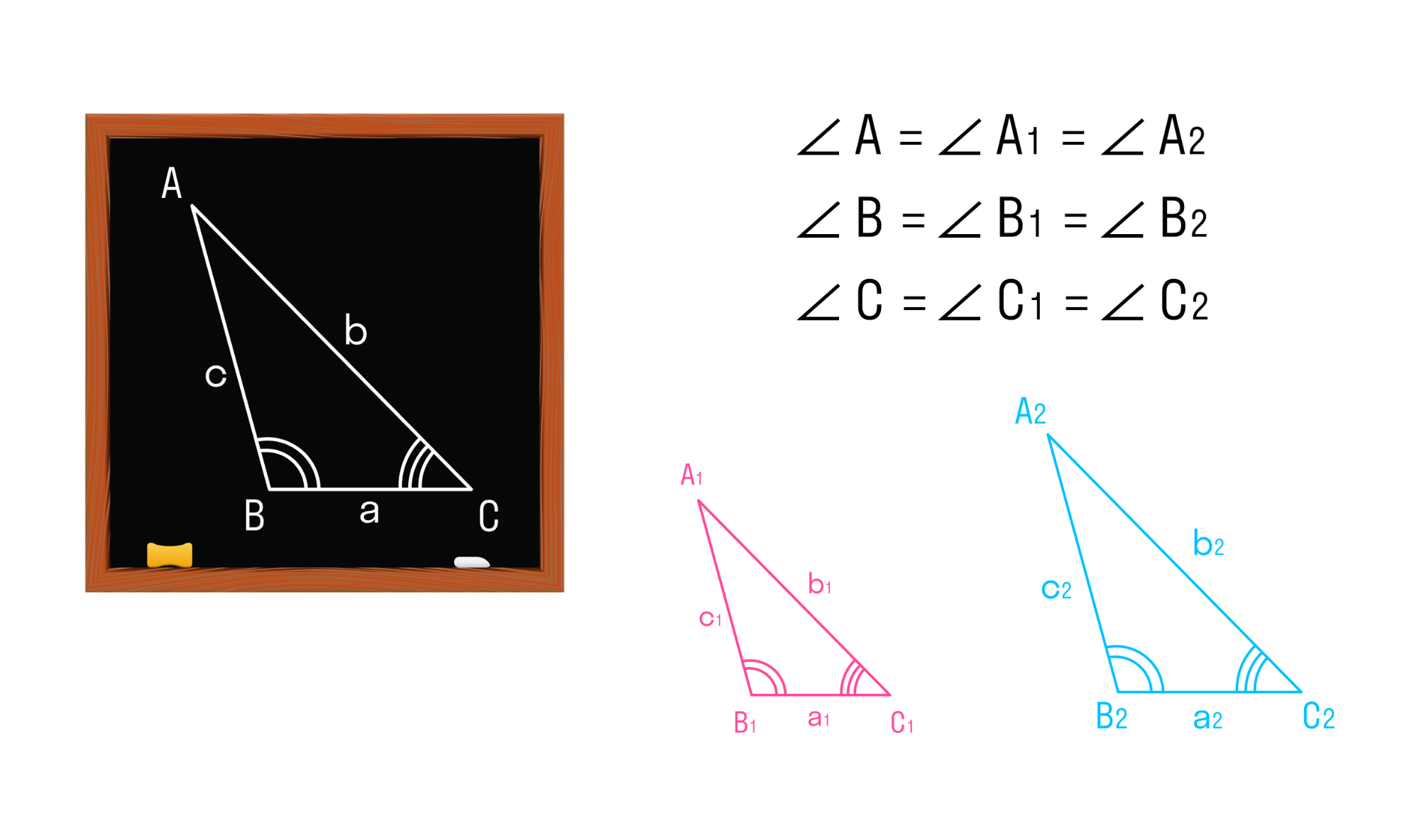
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

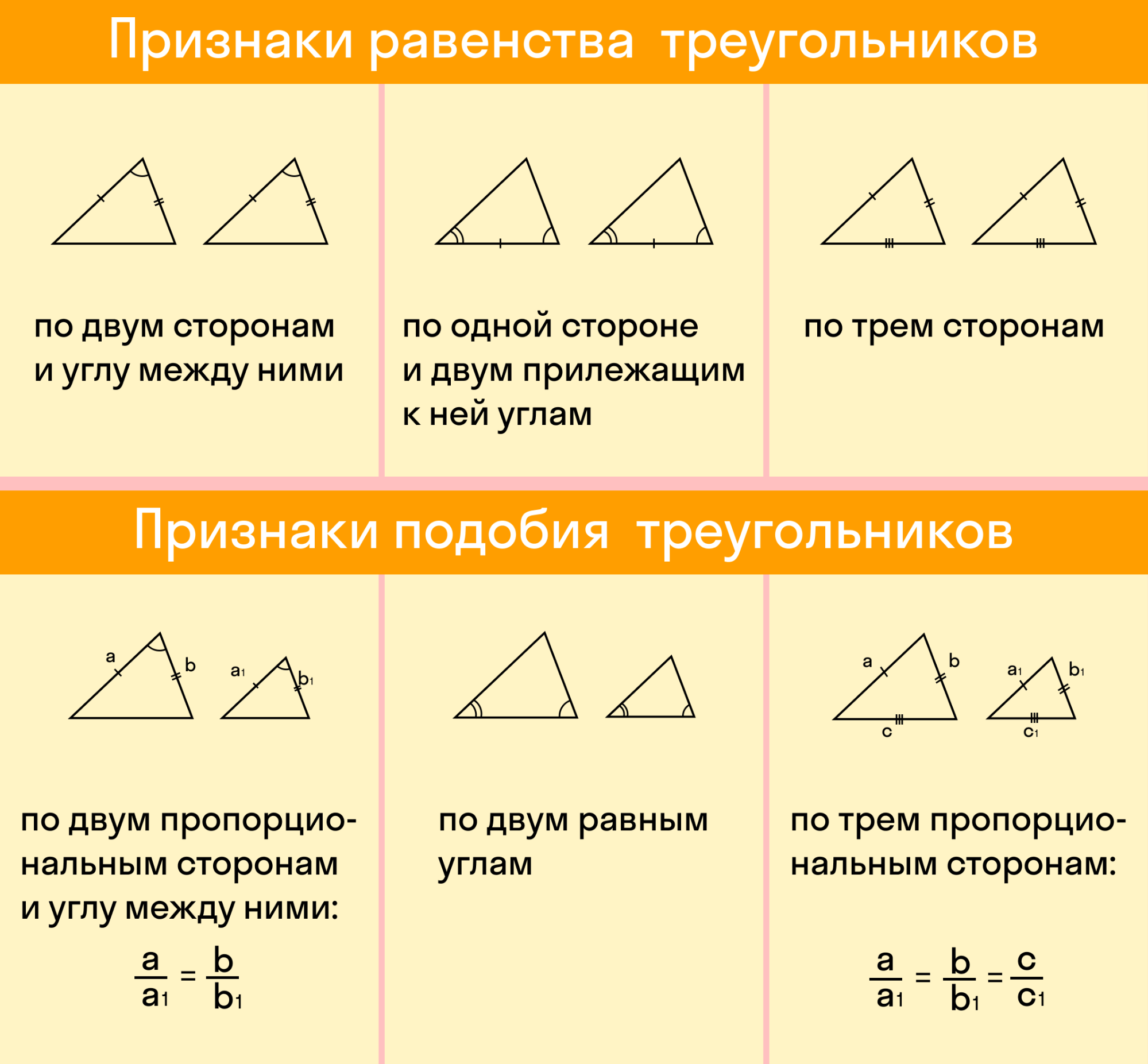
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

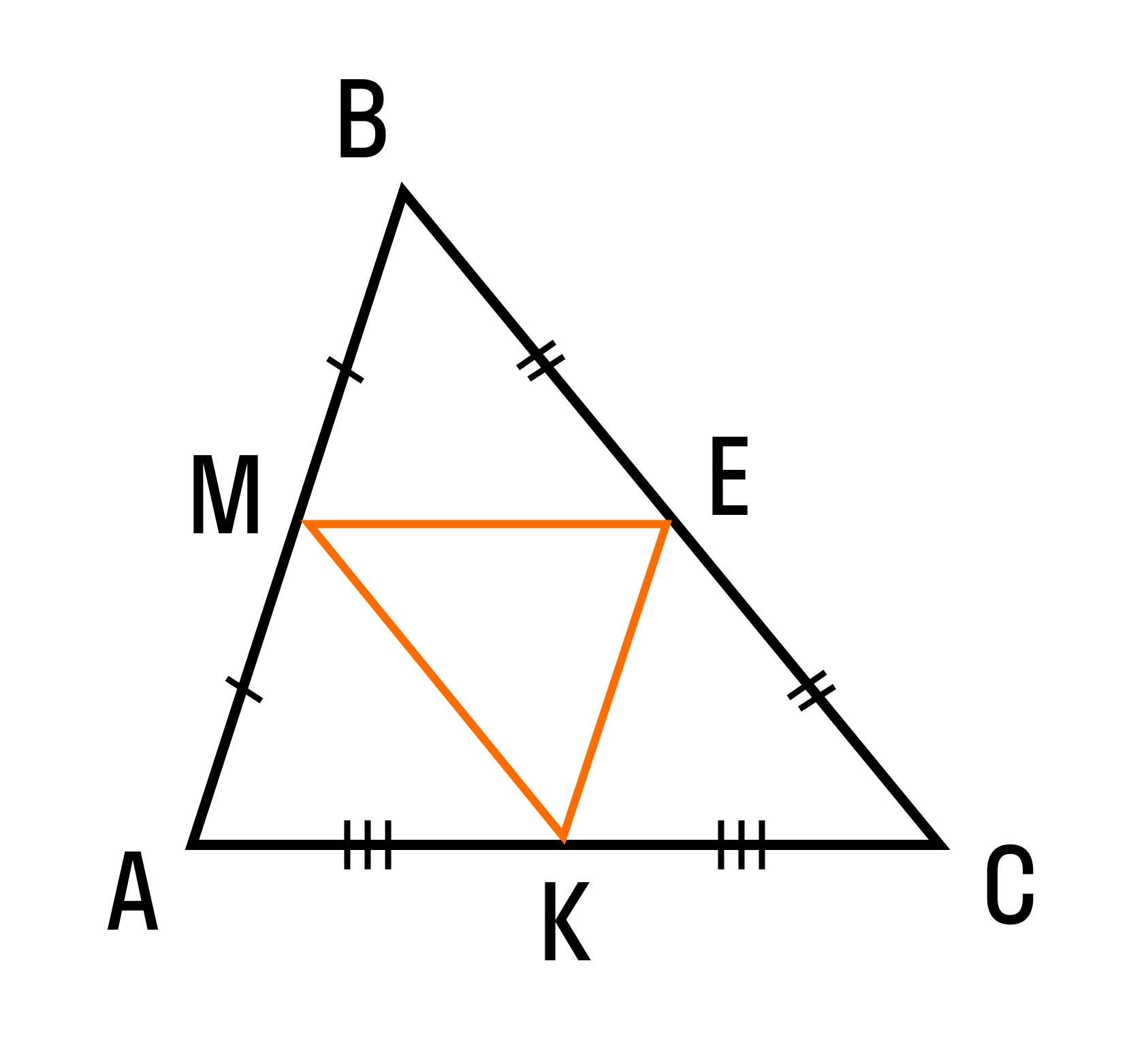
Теорема о средней линии звучит так:

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны

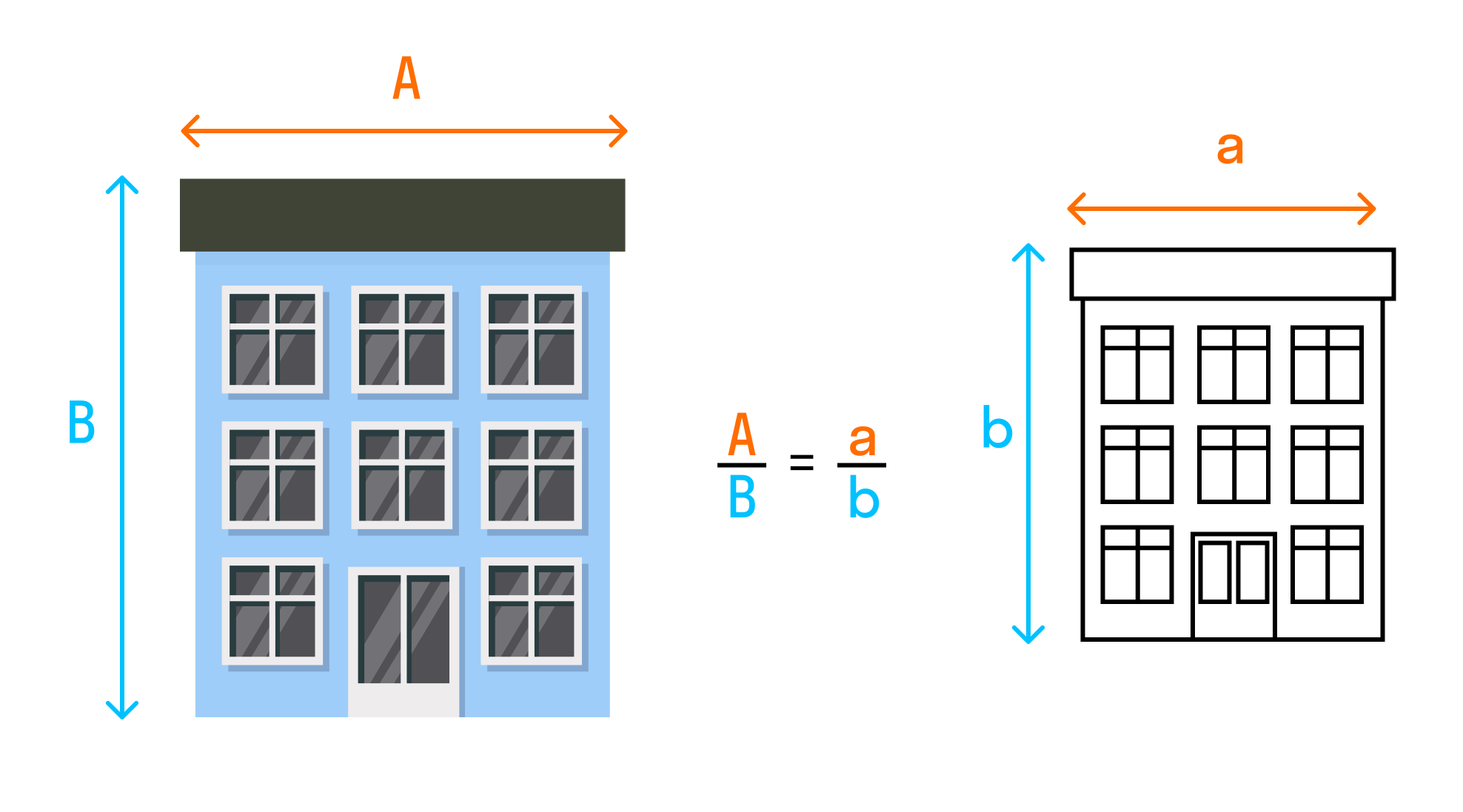
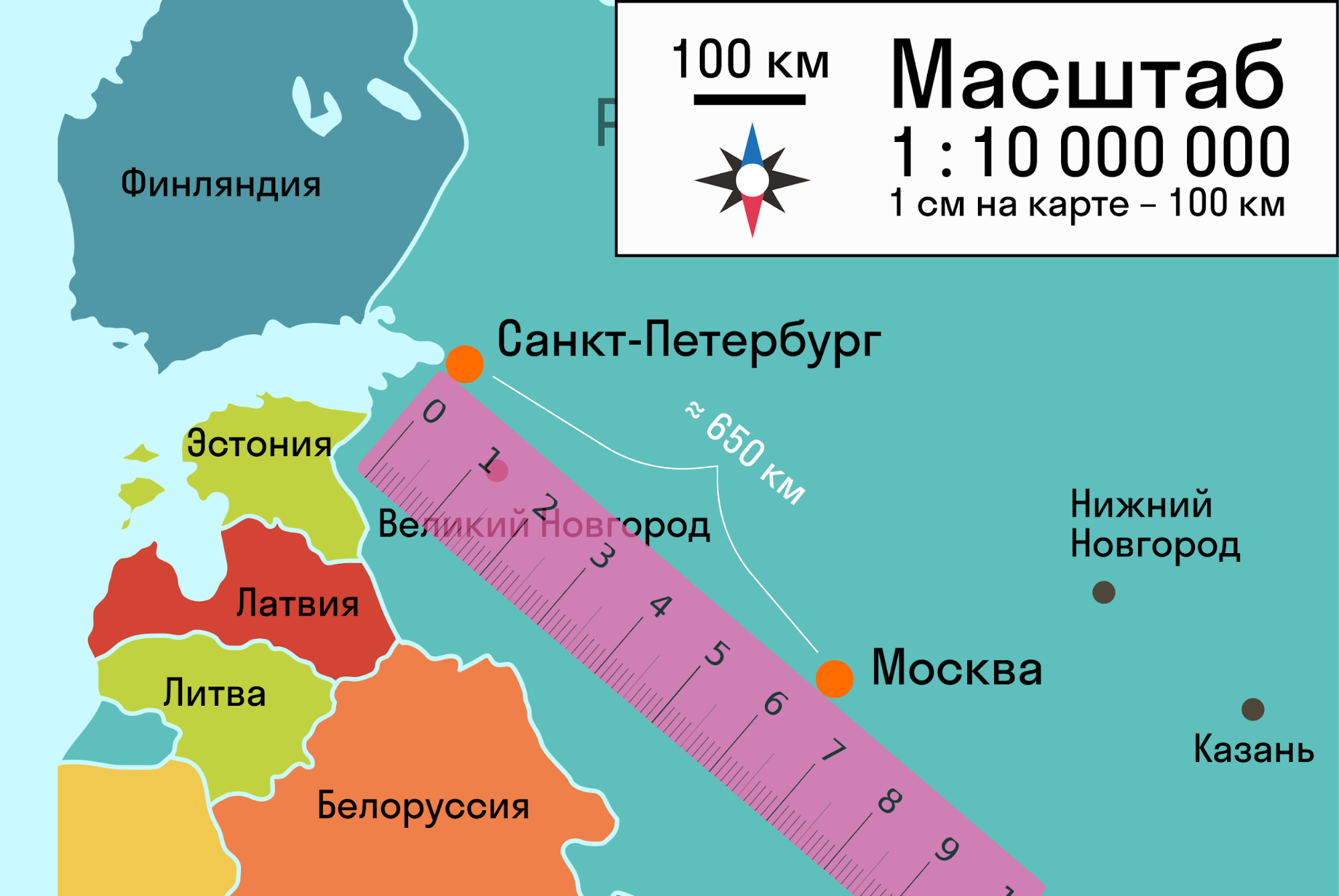
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

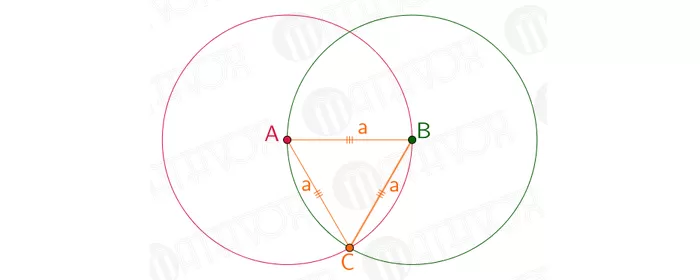
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Kontrolnaya-Rabota.ru

• Построение двухмерного графика функции в декартовых и полярных координатах.
• Построение графика, заданного параметрически.
• Построение 3D графиков (поверхностей), заданных уравнением.
• Построение гистограмм и графиков и по точкам.
• Построение графиков неявно заданных функций.

Пользователю достаточно ввести в онлайн-программу данные из условия задачи и кликнуть кнопку «Построить график».

Запутаться сложно, так как каждая страница этого раздела сопровождается пояснениями и примерами. Там же даны подсказки, какие символы и сокращения следует использовать при вводе выражений.

При построении 2D-графика в декартовых координатах приводится подробный результат исследования функции, чего не встретишь практически нигде.

Достоинства сервиса kontrolnaya-rabota.ru — возможность пользоваться им без ограничений, выдача результатов с ходом решения, быстрые и точные ответы, наличие других онлайн-калькуляторов для вычисления уравнений, интегралов, неравенств и прочего. А недостаток — в том, что не все чертежи можно масштабировать. Это создает определенные неудобства при копировании.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

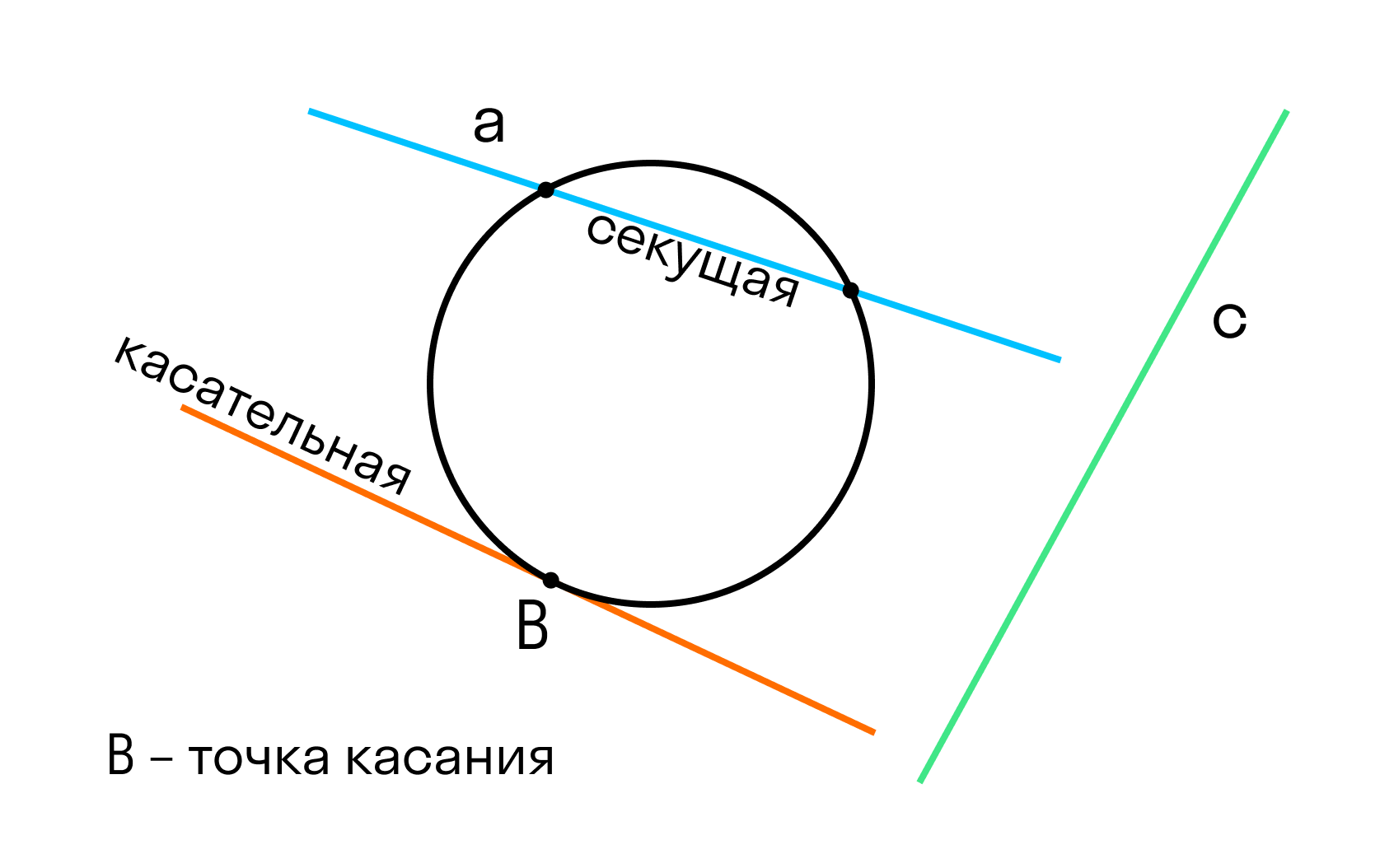
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

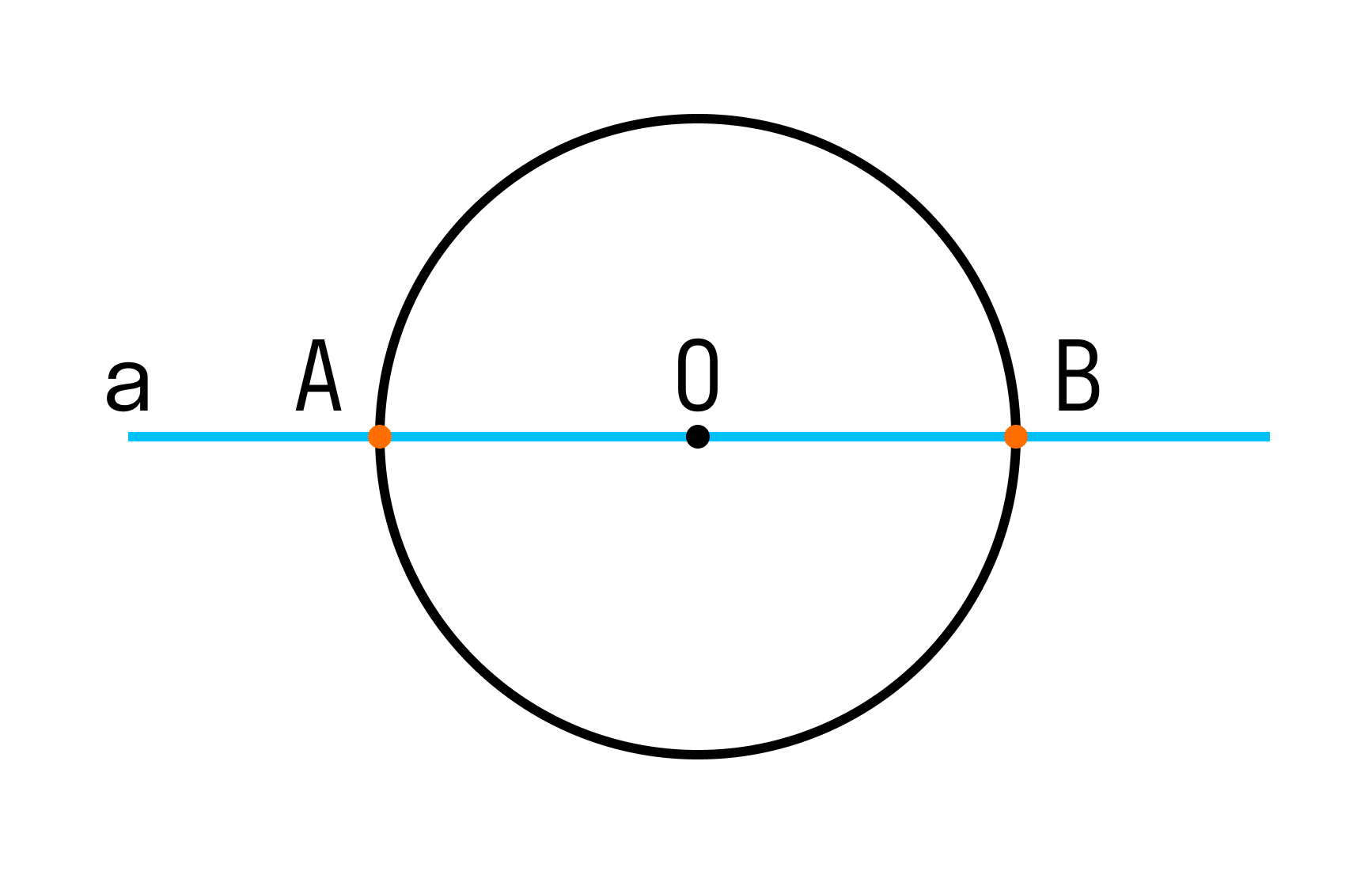
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

• Если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
   
• Если расстояние от центра окружности до прямой равно радиусу окружности (d = r), то прямая и окружность имеют только одну общую точку. В этом случае прямая называется касательной по отношению к окружности.
   
• Если расстояние от центра окружности до прямой больше радиуса окружности (d > r), то прямая и окружность не имеют общих точек.

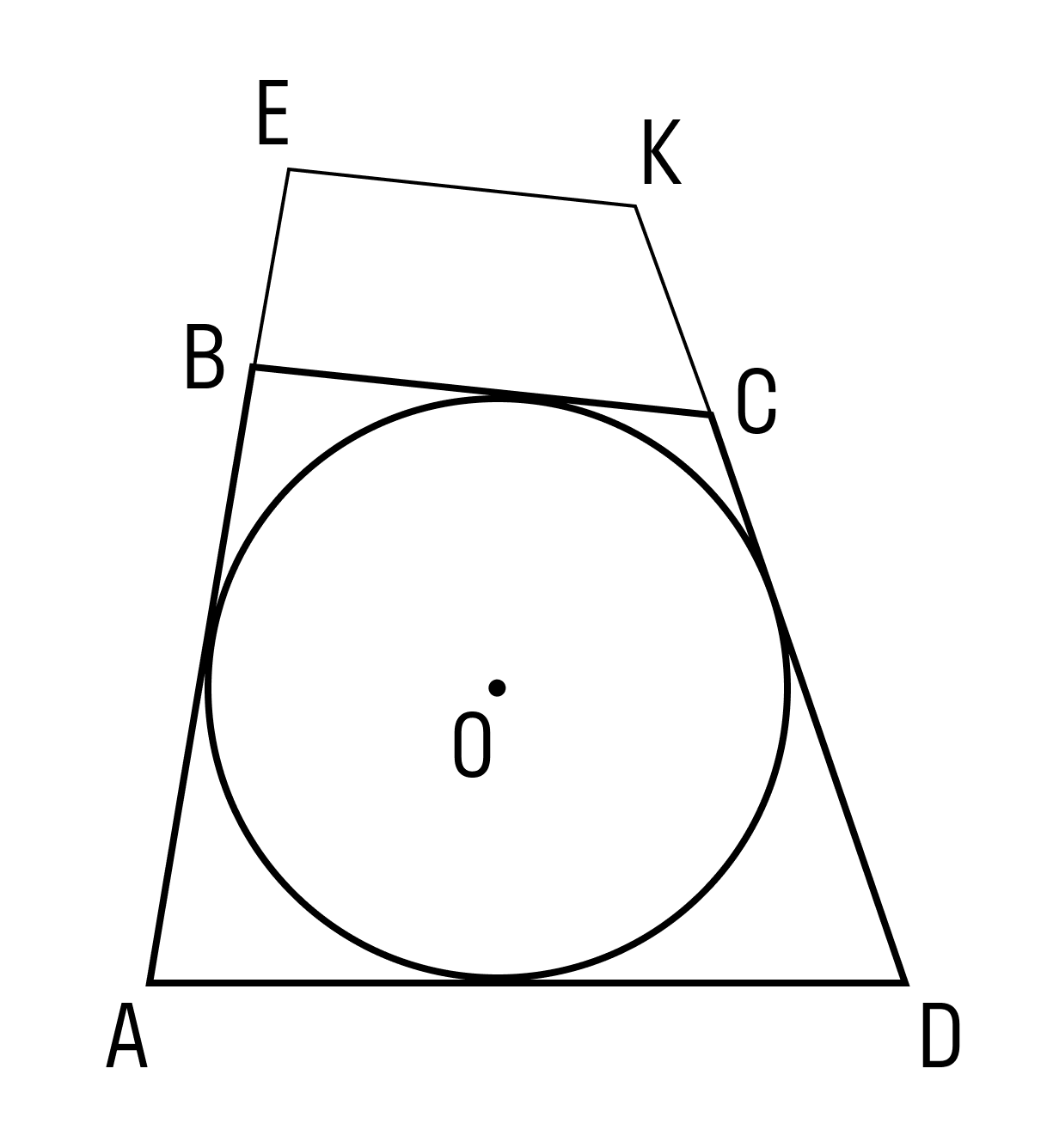
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

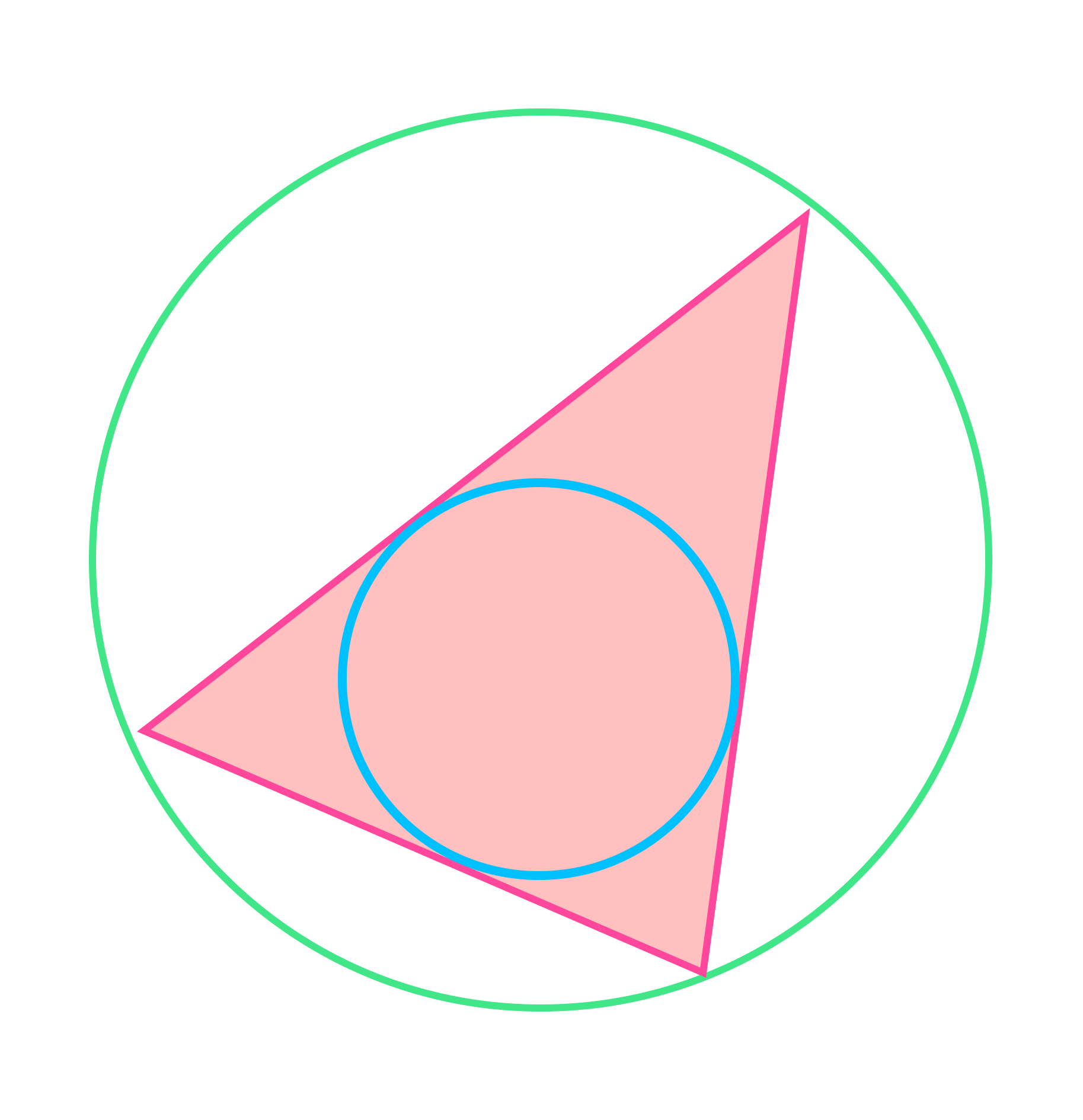
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила. 

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Аналитическая геометрия — Векторы

Векторы

Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.

Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину

Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление

К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».

В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.

Векторный калькулятор	Координаты вектора по двум точкам	Направляющие косинусы вектора
Длина вектора, модуль вектора	Сложение векторов	Вычитание векторов
Умножение вектора на число	Скалярное произведение векторов	Угол между векторами
Проекция вектора на вектор	Векторное произведение векторов	Смешанное произведение векторов
Коллинеарность и ортогональность векторов	Компланарность векторов