How to install numpy

Matplotlib

Matplotlib имеет мощную и при этом еще и красивую визуализацию. Она представляет собой библиотеку построения графиков для Python с 26000 коммитами на GitHub и активным сообществом примерно из 700 участников. Благодаря графикам и чертежам, которые умеет выводить Matplotlib, она широко используется для визуализации данных. Matplotlib также предоставляет объектно-ориентированный API, который можно использовать для встраивания графиков в различные приложения.

Особенности:

• Может использоваться в качестве бесплатной альтернативы MATLAB, с открытым исходным кодом. 
• Поддерживает десятки подчиненных приложений и типов данных для вывода, что означает, что вы можете пользоваться Matplotlib вне зависимости от того какая у вас операционная система и какой формат вы предпочитаете. 
• Pandas может быть использована в качестве оболочки для Matplotlib API для управления Matplotlib, в качестве фильтра. 
• Низкое потребление памяти и хорошая работа во время выполнения.

Области использования:

• Корреляционный анализ переменных. 
• Визуализация интервалов 95-процентной вероятности для моделей. 
• Обнаружение выделяющихся значений с использованием точечной диаграммы и т. п.
• Визуализация распределения данных для получения реальной картины

Видео Top 5 Python Libraries for Data Science демонстрирует простые примеры, которые помогут получить общее представление о возможностях Matplotlib.

Наряду с этими библиотеками специалисты Data Science также используют возможности некоторых других полезных библиотек:

Подобно TensorFlow, Keras — является еще одной популярной библиотекой, которая широко используется для модулей глубокого обучения и нейронных сетей. Keras поддерживает в качестве подчиненного приложения как TensorFlow, так и Theano, поэтому представляет собой хороший вариант, если вы не хотите погружаться в детали TensorFlow.

Scikit-learn — это библиотека машинного обучения, которая предоставляет практически все необходимые алгоритмы машинного обучения. Scikit-learn предназначен для совместной работы с NumPy и SciPy.

Seabourn — еще одна библиотека для визуализации данных. Это расширение matplotlib, предоставляющее дополнительные типы графиков.

Вот видео Simplilearn, в котором рассматриваются 5 лучших библиотек Python для Data Science, созданное экспертами в этой области.

В дополнение к пяти наиболее популярным библиотекам Python и трем другим полезным библиотекам, которые здесь обсуждались, есть много других не менее ценных библиотек для Data Science, заслуживающих вашего внимания. О них вы сможете прочитать в наших следующих статьях.

Скачать

×

Универсальные тригонометрические функции в NumPy

В ходе этой концепции мы теперь рассмотрим некоторые универсальные тригонометрические функции в NumPy .

1. тупица. deg2rad() : Эта функция помогает нам преобразовать значение градуса в радианы.
2. функция numpy.sinh () : Вычисляет значение гиперболического синуса.
3. функция numpy.sin () : Вычисляет обратную гиперболическую величину синуса.
4. функция numpy.hypot () : Вычисляет гипотенузу для прямоугольной структуры треугольника.

Пример:

import numpy as np

data = np.array()

rad = np.deg2rad(data)

# hyperbolic sine value
print('Sine hyperbolic values:')
hy_sin = np.sinh(rad)
print(hy_sin)

# inverse sine hyperbolic
print('Inverse Sine hyperbolic values:')
print(np.sin(hy_sin))

# hypotenuse
b = 3
h = 6
print('hypotenuse value for the right angled triangle:')
print(np.hypot(b, h))

Выход:

Sine hyperbolic values:

Inverse Sine hyperbolic values:

hypotenuse value for the right angled triangle:
6.708203932499369

использованная литература

Работая в качестве исследователя в распределенных системах, доктор Кристиан Майер нашел свою любовь к учению студентов компьютерных наук.

Чтобы помочь студентам достичь более высоких уровней успеха Python, он основал сайт программирования образования Finxter.com Отказ Он автор популярной книги программирования Python One-listers (Nostarch 2020), Coauthor of Кофе-брейк Python Серия самооставленных книг, энтузиаста компьютерных наук, Фрилансера и владелец одного из лучших 10 крупнейших Питон блоги по всему миру.

Его страсти пишут, чтение и кодирование. Но его величайшая страсть состоит в том, чтобы служить стремлению кодер через Finxter и помогать им повысить свои навыки. Вы можете присоединиться к его бесплатной академии электронной почты здесь.

Библиотека Math в Python

Math является самым базовым математическим модулем Python. Охватывает основные математические операции, такие как сумма, экспонента, модуль и так далее. Эта библиотека не используется при работе со сложными математическими операциями, такими как умножение матриц. Расчеты, выполняемые с помощью функций библиотеки math, также выполняются намного медленнее. Тем не менее, эта библиотека подходит для выполнения основных математических операций.

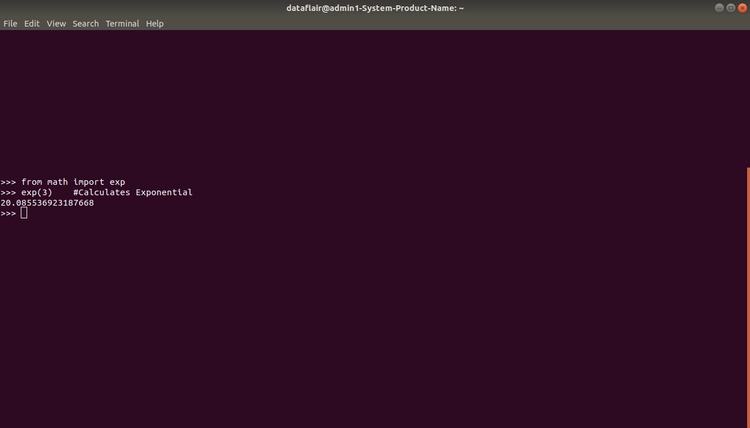
Пример: Вы можете найти экспоненту от 3, используя функцию библиотеки math следующим образом:

Python

from math import exp
exp(3) # Вычисление экспоненты

1 2	frommathimportexp exp(3)# Вычисление экспоненты

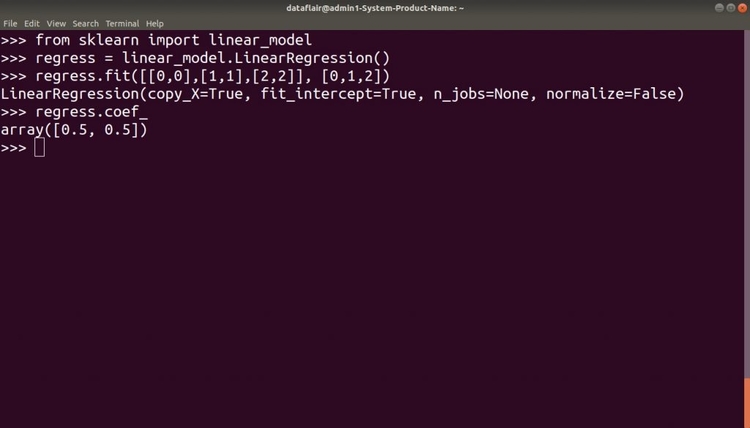
Scikit-learn в Python

Машинное обучение является важным математическим аспектом науки о данных. Используя различные инструменты машинного обучения, вы можете легко классифицировать данные и прогнозировать результаты. Для этой цели Scikit-learn предлагает различные функции, упрощающие методы классификации, регрессии и кластеризации.

Python

from sklearn import linear_model

regress = linear_model.LinearRegression()

regress.fit(,,], )
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

print(regress.coef_) # Результат: array()

1 2 3 4 5 6 7 8 9

fromsklearn importlinear_model regress=linear_model.LinearRegression() regress.fit(,,1,1,2,2,,1,2) LinearRegression(copy_X=True,fit_intercept=True,n_jobs=None,normalize=False) print(regress.coef_)# Результат: array()

Заключение

В данной статье мы рассмотрели важные математические библиотеки Python. Были рассмотрены NumPy, SciPy, statsmodels, а также scikit-learn. В Python есть и другие математические библиотеки, многие находятся в процессе разработки. Надеемся, что определенные моменты руководства вам пригодятся в будущем.

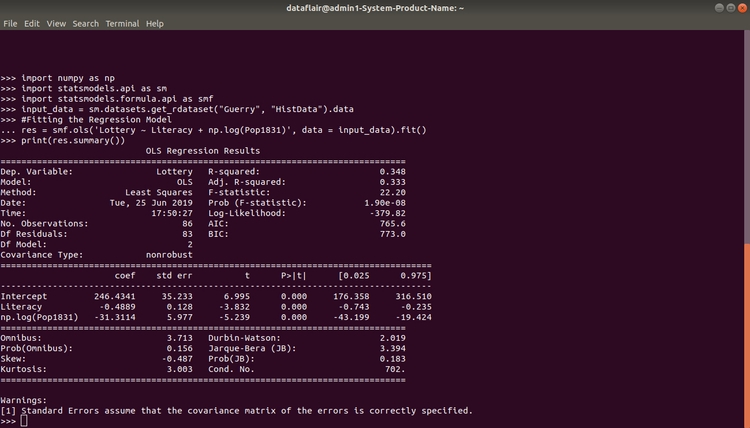
Библиотека Statsmodel в Python

С помощью пакета Statsmodel можно выполнять статистические вычисления, которые включают в себя описательную статистику, логический вывод, а также оценку для различных статистических моделей. Это способствует эффективному статистическому исследованию данных.

Ниже приведен пример реализации библиотеки Statsmodel в Python.

Python

import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf

input_data = sm.datasets.get_rdataset(«Guerry», «HistData»).data

res = smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’, data = input_data).fit()
print(res.summary())

1 2 3 4 5 6 7 8 9

importnumpy asnp importstatsmodels.api assm importstatsmodels.formula.api assmf input_data=sm.datasets.get_rdataset(«Guerry»,»HistData»).data res=smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’,data=input_data).fit() print(res.summary())

Арифметические операции над массивами NumPy

Создадим два массива NumPy и продемонстрируем выгоду их использования.

Массивы будут называться и :

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать :

Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.

Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию :

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.

DataFrame

DataFrame – самая важная и широко используемая структура данных, а также стандартный способ хранения данных. Она содержит данные, выровненные по строкам и столбцам, как в таблице SQL или в базе данных электронной таблицы.

Мы можем либо жестко закодировать данные в DataFrame, либо импортировать файл CSV, файл tsv, файл Excel, таблицу SQL и т.д.

Мы можем использовать приведенный ниже конструктор для создания объекта DataFrame.

pandas.DataFrame(data, index, columns, dtype, copy)

Ниже приводится краткое описание параметров:

• data – создать объект DataFrame из входных данных. Это может быть список, dict, series, Numpy ndarrays или даже любой другой DataFrame;
• index – имеет метки строк;
• columns – используются для создания подписей столбцов;
• dtype – используется для указания типа данных каждого столбца, необязательный параметр;
• copy – используется для копирования данных, если есть.

Есть много способов создать DataFrame. Мы можем создать объект из словарей или списка словарей. Мы также можем создать его из списка кортежей, CSV, файла Excel и т.д.

Давайте запустим простой код для создания DataFrame из списка словарей.

import pandas as pd
import numpy as np
df = pd.DataFrame({
    "State": ,
    "Capital": ,
    "Literacy %": ,
    "Avg High Temp(c)": 
})
print(df)

Вывод:

Первый шаг – создать словарь. Второй шаг – передать словарь в качестве аргумента в метод DataFrame(). Последний шаг – распечатать DataFrame.

Как видите, DataFrame можно сравнить с таблицей, имеющей неоднородное значение. Кроме того, можно изменить размер.

Мы предоставили данные в виде карты, и ключи карты рассматриваются Pandas, как метки строк.

Индекс отображается в крайнем левом столбце и имеет метки строк. Заголовок столбца и данные отображаются в виде таблицы.

Также возможно создавать индексированные DataFrames. Это можно сделать, настроив параметр индекса.

Линейная алгебра

SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.

Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.

Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.

Этот метод ожидает входную матрицу и вектор правой части:

# Import required modules/ libraries
import numpy as np
from scipy import linalg

# We are trying to solve a linear algebra system which can be given as:
#               1x + 2y =5
#               3x + 4y =6

# Create input array
A= np.array(,])

# Solution Array
B= np.array(,])

# Solve the linear algebra
X= linalg.solve(A,B)

# Print results
print(X)

# Checking Results
print("\n Checking results, following vector should be all zeros")
print(A.dot(X)-B)

Транспонирование и изменение формы матриц в numpy

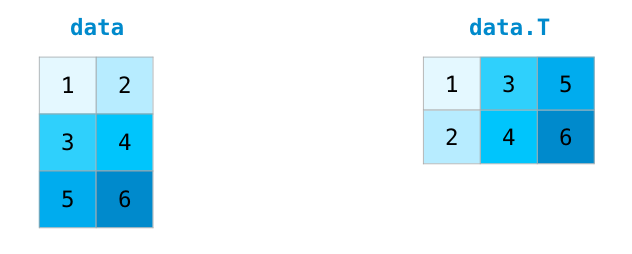
Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.

Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:

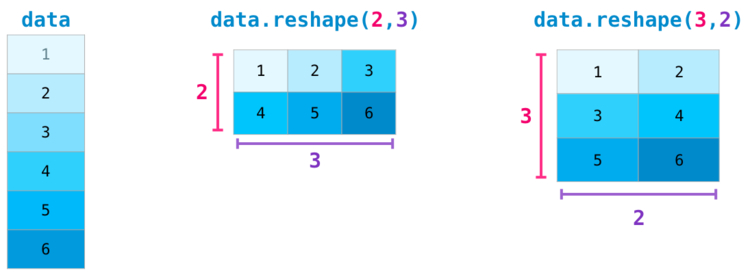
Еще больше размерностей NumPy

NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.

В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:

Shell

array(,
,
],

,
,
],

,
,
],

,
,
]])

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.)

Сбор данных

Наука о данных включает в себя обработку данных, чтобы данные могли хорошо работать с алгоритмами данных. Data Wrangling – это процесс обработки данных, такой как слияние, группировка и конкатенация.

Библиотека Pandas предоставляет полезные функции, такие как merge(), groupby() и concat() для поддержки задач Data Wrangling.

import pandas as pd

d = {  
    'Employee_id': ,
    'Employee_name': 
}
df1 = pd.DataFrame(d, columns=)  
print(df1)

import pandas as pd

data = {  
    'Employee_id': ,
    'Employee_name': 
}
df2 = pd.DataFrame(data, columns=)  
print(df2)

а. merge()

print(pd.merge(df1, df2, on='Employee_id'))

Мы видим, что функция merge() возвращает строки из обоих DataFrames, имеющих то же значение столбца, которое использовалось при слиянии.

b. Группировка

import pandas as pd
import numpy as np

data = {
    'Employee_id': ,
    'Employee_name': 
}
df2 = pd.DataFrame(data)

group = df2.groupby('Employee_name')
print(group.get_group('Meera'))

Поле «Employee_name» со значением «Meera» сгруппировано по столбцу «Employee_name». Пример вывода приведен ниже:

Тест производительности

Мы не должны чередовать векторизованную операцию numpy вместе с циклом. Это резко снижает производительность, так как код повторяется с использованием собственного.

Например, в приведенном ниже фрагменте показано, как не следует использовать numpy.

for i in np.arange(100):
    pass

Рекомендуемый способ – напрямую использовать операцию numpy.

np.arange(100)

Давайте проверим разницу в производительности с помощью модуля timeit.

import timeit
import numpy as np

# For smaller arrays
print('Array size: 1000')

# Time the average among 10000 iterations
print('range():', timeit.timeit('for i in range(1000): pass', number=10000))
print('np.arange():', timeit.timeit('np.arange(1000)', number=10000, setup='import numpy as np'))

# For large arrays
print('Array size: 1000000')

# Time the average among 10 iterations
print('range():', timeit.timeit('for i in range(1000000): pass', number=10))
print('np.arange():', timeit.timeit('np.arange(1000000)', number=10, setup='import numpy as np'))

Вывод:

Array size: 1000
range(): 0.18827421900095942
np.arange(): 0.015803234000486555
Array size: 1000000
range(): 0.22560399899884942
np.arange(): 0.011916546000065864

Как видите, numpy.arange() особенно хорошо работает для больших последовательностей. Это почти в 20 раз (!!) быстрее обычного кода Python для размера всего 1000000, который будет лучше масштабироваться только для больших массивов.

Следовательно, numpy.arange() должен быть единодушным выбором среди программистов при работе с большими массивами. Для небольших массивов, когда разница в производительности не так велика, вы можете использовать любой из двух методов.

Как работает NumPy

Для начала разберемся в устройстве массивов, которые обрабатывает NumPy. Рассмотрим однородный двумерный массив. Он выглядит как простая таблица — две оси значений и ячейки внутри (элементы массива). Если появится третья ось, то массив станет трехмерным

Важное условие — все элементы должны иметь единый тип данных, например только целые числа

Пример визуализации двумерного массива

Конечно, кроме двумерных массивов, библиотека NumPy обрабатывает и другие, с различным количеством осей. Эту вариативность обозначают числом N, как любую переменную в математической задаче. Поэтому обычно говорят, что NumPy работает с N-мерными массивами данных.

С этими данными NumPy производит вычисления, используя математические функции, генераторы случайных чисел, линейные уравнения или преобразования Фурье. Например, можно решить систему уравнений методом linalg.solve:

import numpy as npleft = np.array( , ] )right = np.array( )np.linalg.solve(left, right)Ответ: array()

Как и сам Python, библиотека NumPy отличается простотой в изучении и использовании. Для начала работы достаточно освоить концепцию массивов. Например, в базовых арифметических вычислениях есть способ обработки массивов, который называют ‎трансляцией‎ или broadcasting.

Если в массиве величины указаны в милях, а результат нужно получить в километрах, можно умножить его на простое число 1,6 (скалярную величину). NumPy принимает самостоятельное решение умножить на заданное число каждый элемент в массиве, и пользователю не приходится прописывать для этого отдельную команду.

Подробной документации NumPy на русском языке до сих пор нет, а в рунете можно найти только краткие выжимки, в которых упущены многие моменты. Поэтому, чтобы стать специалистом высокого уровня в Data Science или Machine Learning, придется подтянуть английский. Начать можно с информации на официальном сайте.

Курс

Python для аналитики данных

Вы сможете автоматизировать сбор и анализ данных о ваших конкурентах, пользователях и потенциальных партнерах с помощью Python. Дополнительная скидка 5% по промокоду BLOG.

Узнать больше

Тригонометрические функции

Конечно, любой
состоятельный математический пакет должен иметь в своем составе
тригонометрические функции и NumPyздесь не исключение. Наиболее
употребительные из них приведены в следующей таблице:

Название	Описание
np.sin(x)	Вычисление синуса угла x (в радианах); xможет быть числом, списком, массивом (это правило распространяется на все функции этой таблицы).
np.cos(x)	Вычисление косинуса угла(ов) x.
np.tan(x)	Вычисление тангенса угла(ов) x.
np.arccos(x)	Арккосинус угла(ов) x.
np.arcsin(x)	Арксинус угла(ов) x.
np.arctan(x)	Арктангенс угла(ов) x.

Их использование
также вполне очевидно. На входе они могут принимать массив, список или число.
Если это угол, то он представляется в радианах. Например:

a = np.linspace(, np.pi, 10)
res1 = np.sin(a) # возвращает массив синусов углов
np.sin(np.pi/3)
np.cos(, 1.57, 3.17)
res2 = np.cos(a) # возвращает массив косинусов углов
np.arcsin(res1) # возвращает арксинусы от значений res1

Причем, все эти
функции работают быстрее аналогичных функций языка Python. Поэтому, при
использовании библиотеки NumPy предпочтение лучше отдавать именно ей,
а не языку Python при
тригонометрических вычислениях.

Создание десктопных приложений и UI

EEL

Для работы с созданием графических приложений есть несколько популярных библиотек, в частности встроенный tkinter и Qt. Но когда необходимо сделать красивое, легковесное графическое приложение, то хотелось бы использовать что-то более мощное, например, html+css+js, именно с этим может помочь библиотека EEL. Она позволяет создать десктопное приложение, где в качестве графической оболочки используется html, css и js (можно использовать различные фреймворки), а в качестве языка для написания бэк-части используется Python (подробнее тут).

Приведем простой пример использования библиотеки. Python код:

Файл index.html:

И сама структура проекта должна выглядеть так:

Можно запустить файл main.py и убедиться, что всё работает:

Функции sum, mean, min и max

Итак, очень
часто на практике требуется вычислять сумму значений элементов массива, их
среднее значение, а также находить минимальные и максимальные значения. Для
этих целей в NumPy существуют
встроенные функции, выполняющие эти действия и сейчас мы посмотрим как они
работают. Пусть, как всегда, у нас имеется одномерный массив:

a = np.array( 1,  2,  3, 10, 20, 30)

Вычислим сумму,
среднее значение и найдем максимальное и минимальное значения:

a.sum()    # 66
a.mean()  # 11.0
a.max()    # 30
a.min()    # 1

Как видите, все
достаточно просто. Тот же самый результат будет получен и при использовании
многомерных массивов. Например:

a.resize(3, 2)
a.sum()  # 66

Но, если
требуется вычислить сумму только по какой-то одной оси, то ее можно явно
указать дополнительным параметром:

a.sum(axis=)  # array()
a.sum(axis=1) # array()

Точно также
работают и остальные три функции, например:

a.max(axis=)  # array()
a.min(axis=1)  # array()

Other Useful Items

• Looking for 3rd party Python modules? The
  Package Index has many of them.
• You can view the standard documentation
  online, or you can download it
  in HTML, PostScript, PDF and other formats. See the main
  Documentation page.
• Information on tools for unpacking archive files
  provided on python.org is available.
• Tip: even if you download a ready-made binary for your
  platform, it makes sense to also download the source.
  This lets you browse the standard library (the subdirectory Lib)
  and the standard collections of demos (Demo) and tools
  (Tools) that come with it. There’s a lot you can learn from the
  source!
• There is also a collection of Emacs packages
  that the Emacsing Pythoneer might find useful. This includes major
  modes for editing Python, C, C++, Java, etc., Python debugger
  interfaces and more. Most packages are compatible with Emacs and
  XEmacs.

Арифметические операции с матрицей

Вы можете выполнять арифметические операции, такие как сложение, вычитание, умножение и деление между матрицами. В следующем примере вы можете увидеть несколько примеров арифметических операций.

import numpy


# initialize two array
x = numpy.array(, ], dtype=numpy.float64)
y = numpy.array(, ], dtype=numpy.float64)

print('Print the two matrices')
print('X = \n', x)
print('Y = \n', y)

# Elementwise sum; both produce the array
print('\nElementwise addition of two matrices: ( X + Y of Matlab )')
print('Add using add operator: \n', x + y)
print('Add using add function: \n', numpy.add(x, y))

# Elementwise difference; both produce the array
print('\nElementwise subtraction of two matrices: ( X - Y of Matlab )')
print('Subtract using operator: \n', x - y)
print('Subtract using function: \n', numpy.subtract(x, y))

# Elementwise product; both produce the array
print('\nElementwise Multiplication of two matrices: ( X .* Y of Matlab )')
print('Multiply using operator: \n', x * y)
print('Multiply using function: \n', numpy.multiply(x, y))

# Elementwise division; both produce the array
print('\nElementwise division of two matrices: ( X ./ Y of Matlab )')
print('Division using operator: \n', x / y)
print('Division using function: \n', numpy.divide(x, y))

# Elementwise square root; produces the array
print('\nSquare root each element of X matrix\n', numpy.sqrt(x))

# Matrix Multiplication
print('\nMatrix Multiplication of two matrices: ( X * Y of Matlab )')
print(x.dot(y))

Ниже приведен результат работы вышеуказанной программы матрицы numpy.

X = 
 
 ]
Y = 
 
 ]

Elementwise addition of two matrices: ( X + Y of Matlab )
Add using add operator: 
 
 ]
Add using add function: 
 
 ]

Elementwise subtraction of two matrices: ( X - Y of Matlab )
Subtract using operator: 
 
 ]
Subtract using function: 
 
 ]

Elementwise Multiplication of two matrices: ( X .* Y of Matlab )
Multiply using operator: 
 
 ]
Multiply using function: 
 
 ]

Elementwise division of two matrices: ( X ./ Y of Matlab )
Division using operator: 
 
 ]
Division using function: 
 
 ]

Square root each element of X matrix
 
 ]

Matrix Multiplication of two matrices: ( X * Y of Matlab )

 ]

Upgrading NumPy

If you already have NumPy and want to upgrade to the latest version, for Pip2 use the command:

If using Pip3, run the following command:

Conclusion

By following this guide, you should have successfully installed NumPy on your system.

Check out our introduction tutorial on Python Pandas, an open-source Python library primarily used for data analysis, which is built on top of the NumPy package and is compatible with a wide array of existing modules. The collection of tools in the Pandas package is an essential resource for preparing, transforming, and aggregating data in Python.

For more Python package tutorials, check out our other KB articles such as Best Python IDEs and more!

Аргумент ключевого слова axis

Это устанавливает axis для сохранения образцов. Он используется только в том случае, если начальная и конечная точки относятся к типу данных массива.

По умолчанию (axis = 0) образцы будут располагаться вдоль новой оси, вставленной в начало. Мы можем использовать axis = -1, чтобы получить ось в конце.

import numpy as np

p = np.array(, ])
q = np.array(, ])

r = np.linspace(p, q, 3, axis=0)
print(r)
s = np.linspace(p, q, 3, axis=1)
print(s)

Вывод

array(,
        ],

       ,
        ],

       ,
        ]])

array(,
        ,
        ],

       ,
        ,
        ]])

В первом случае, поскольку axis = 0, мы берем пределы последовательности от первой оси.

Здесь пределы – это пары подмассивов и , а также и , берущие элементы из первой оси p и q. Теперь мы сравниваем соответствующие элементы из полученной пары, чтобы сгенерировать последовательности.

Таким образом, последовательности , ] для первой строки и ], ] для второй пары (строки), которая оценивается и объединяется для формирования , ], , ], , ]],

Во втором случае будут вставлены новые элементы в axis = 1 или столбцы. Таким образом, новая ось будет создана через последовательности столбцов. вместо последовательностей строк.

Последовательности с по и по рассматриваются и вставляются в столбцы результата, в результате чего получается , , ], , , ]].

Будучи генератором линейной последовательности, функция numpy.arange() в Python используется для генерации последовательности чисел в линейном пространстве с равномерным размером шага.

Это похоже на другую функцию, numpy.linspace() в Python, которая также генерирует линейную последовательность с одинаковым размером шага.

Давайте разберемся, как мы можем использовать эту функцию для генерации различных последовательностей.